
黄陂区实验中学教师方铭。
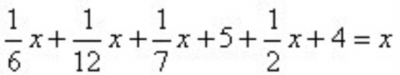
图一
图二
名师名片:方铭,黄陂区实验中学高级教师,两次参加武汉市中考数学命题工作,两次参加教学比武均荣获武汉市一等奖,黄陂区初中数学学科带头人。
————————
学习的兴趣总是在情景中发生的,离开了情景,学习就很盲目。数学不是枯燥的,更不是无用的,生活中处处皆情景,处处是数学。情景化学习是破解“数学无用论”的金钥匙。在数学学习活动中,同学们该如何进行情景化学习呢?
■ 问题式情景化学习
学源于思,思始于疑。面对新知学习的时候,学生如果能够把数学问题代入到生活情景中,那么学习起来会起到事半功倍的效果。
如进行勾股定理学习时,可能会面对这样一个问题:马戏团的一只猴子在进行爬梯表演,梯子的长度是5米,梯子摆放时,它的水平距离是3米,假设该小猴在4.5米的高度范围内落下不会受伤。如果这只小猴表演时爬到该梯子的顶端不慎落下,那么猴子会不会有危险?
学习开始,同学们你一言我一语,但是没有一个明确的结果,最后可能会陷入片刻的沉思之中,而恰恰是此时,学生们的思维却是最活跃的。这时老师如果迅速切入主题,稍作点拨,学生就能醍醐灌顶,学以致用。
■ 故事式情景化学习
在学习列方程解应用题的时候,很多同学还局限在小学的算术解决方法,看不到列方程求解的优点。如果碰到了下面这个问题,学生就会感受到算术方法的局限性,从而激起对方程学习的兴趣。
相传在古希腊数学家丢番图的墓碑上,记载着这样一道谜语般的数学题:他生命的六分之一是幸福的童年,再过十二分之一,脸上长起了细细的胡须,他结了婚还没有孩子,又度过了七分之一,再过了五年,他得到了一个儿子,可这孩子的寿命只有他父亲的一半,儿子死后,老人在悲痛中活了四年就去世了。请问数学家丢番图活了多少岁?他结婚时多少岁?
面对这道题,学生习惯的算术方法就不奏效了,而此时列方程来解决却是易如反掌。设他活了x岁,依题意有(图一):
这样,要知道丢番图的年纪,只要解出这个方程就行了。这段墓志铭写得太妙了,谁想知道丢番图的年纪,就得解一个一元一次方程,而这又正好提醒前来瞻仰的人们,不要忘记了丢番图献身代数事业的故事。
■ 游戏式情景化学习
学生在游戏时常常能达到忘我的境界,他们主动参与游戏,兴致勃勃,在这一过程中游戏的趣味性是诱发兴趣的关键。其实,一些游戏过程中涉及方案选择的时候,也是需要数学知识作为理论支撑的。
如在进行概率学习时会碰到这样一个问题:计算机的扫雷游戏中,小明随机点开了一个方格,点击后出现数字3,我们把以“3”为中心的9个方格框起来记为A区域,A区域以外的记为B区域。数字3表示A区域有三颗地雷,踩雷则游戏结束,下一步该点击A区域还是B区域?
如果根据地雷的数字来看,应选择A区,如果从非雷区域面积来看,应选择B区。但是生活、游戏的背后其实蕴藏着数学原理,那么站在数学的角度,如何通过数据分析,来进行科学的选择呢?面对这个问题,学生发现只有学好数学,学会概率后,才能更好地去玩游戏。这样的情景,会让学生对新知产生强烈的共鸣。
■ 生活中的情景化学习
在生活中,经常会碰到最佳方案选择的问题,这时候,如果学生能够运用建模的思想,将生活问题转化成数学中的函数模型,那么便会迅速发现最佳方案。
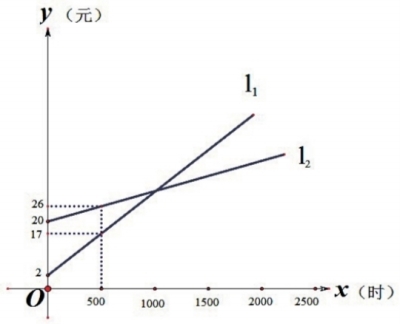
如图(图二),l1、l2分别表示一种白炽灯和一种节能灯的费用(费用=灯的售价+电费,单位:元)与照明时间x(时)的函数图像,假设两种灯的使用寿命都是2500小时,照明效果一样。如果小亮的房间计划照明2000小时,那么他最好买哪种型号的灯呢?
我们先分别求出l1、l2的函数解析式y1=0.03x+2,y2=0.012x+20,会发现:当使用时间为1000小时时,二者费用一样y1=y2=32元;当使用少于1000小时时,应选择白炽灯;当使用超过1000而又少于2500小时时,应选择节能灯。
那么最合理的方案不言而喻了。通过对这个问题的学习,学生们更加明白了只有学好数学,才能运用数学智慧选择最佳方案。
■ 德育中的情景化学习
数学是比较难学好的科目,尤其是到了八年级,数学思想方法多了,知识也变难了,因此有些同学就退缩了,尤其是形象思维能力较强而逻辑思维能力较差的部分女生。因此,在平时的课堂上,同学们既要学习数学知识,还要学习数学家们不畏困难、刻苦钻研的精神和品质,这样才能保持自己旺盛的学习热情和持久的学习动力。
如屈居于六平方米小屋的陈景润,借一盏昏暗的煤油灯,伏在床板上,用一支笔,历时多年并耗去了几麻袋的草稿纸,最终攻克了世界著名数学难题“哥德巴赫猜想”中的(1+2),创造了距离摘取这颗数论皇冠上的明珠(1+1)只有一步之遥的辉煌,被国际数学界誉为“陈氏定理”。数学家的故事告诉我们,真正的成功源于对梦想的执着与纯粹的热爱,他们的精神值得每一位追求卓越的人学习。
情景创设不是简单地给数学“披上生活的外衣”,而是重构数学学习生态的支点,是实现学科隔离到学科融合的桥梁。作为学生,在数学学习中要充分借助情景,将数学问题代入到情景中进行沉浸式体验,体会数学知识的魅力,感受学以致用的快乐。
